原理介绍
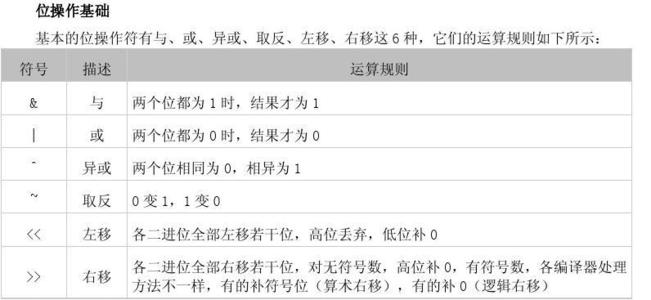
Bit Operation:位运算,程序中的所有数在计算机内存中都是以二进制的形式储存的,位运算就是直接对整数在内存中的二进制位进行操作,所以运算速度相对较快。位运算主要包括**按位与(&)、按位或(|)、按位异或(^)、取反()、左移(<<)**、**右移(>>)**这几种,其中除了取反()以外,其他的都是二目运算符,即要求运算符左右两侧均有一个运算量。
算法基础
原码
原码是二进制的一种表现方式。取该整数的绝对值的二进制,再加上符号位。该原码只是为了让我们看二进制更直观,直接看出正负数和比较大小。但原码不是计算机保存的二进制,所以不能直接参与计算。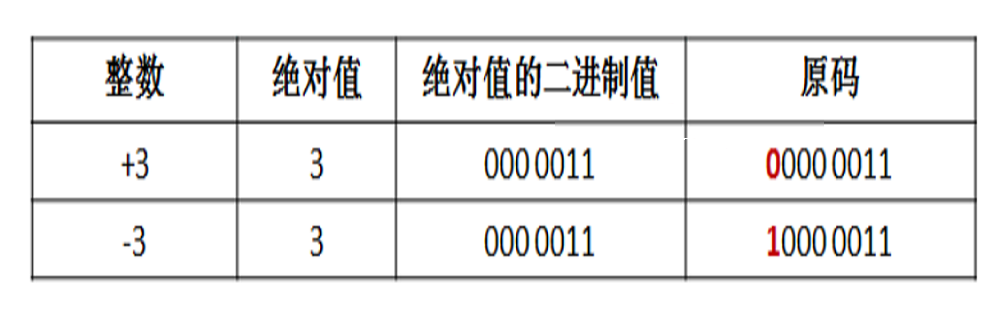
反码
反码主要是针对负数的处理。非负数的反码等于其原码,负数的反码在原码的基础上,符号位不变,其他数值位取反,即把1变成0,把0变成1。反码是为了在计算机中存储二进制,但非真正的二进制值,所以也不直接参与计算。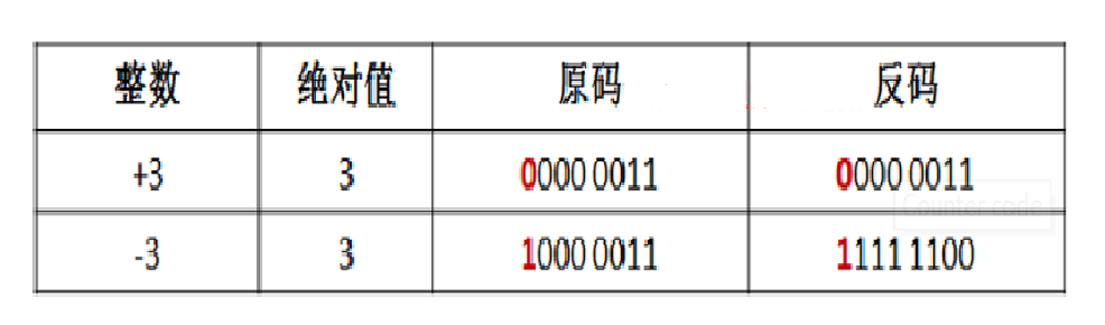
补码
补码是真正的二进制值了,主要也是针对负数。非负数不变,而负数是在反码的基础上加1,为了方便正数和负数之间进行运算。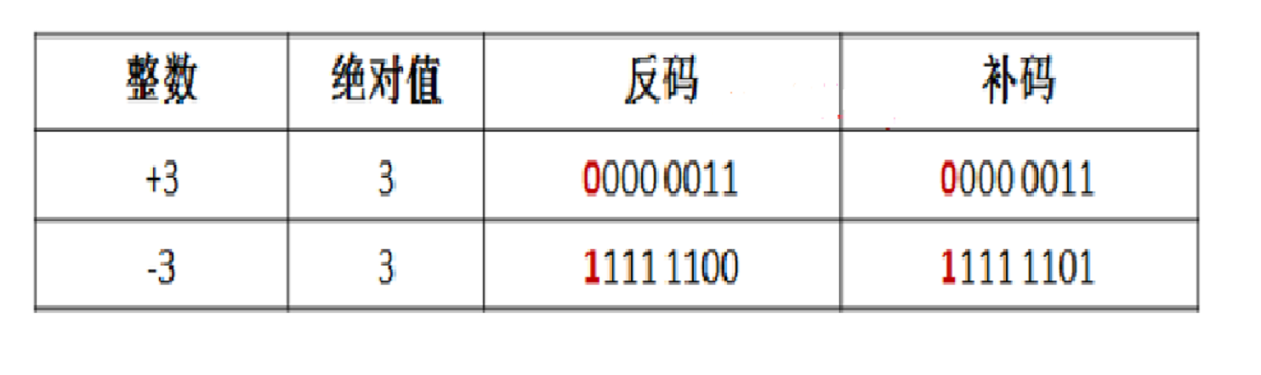
位运算
位运算技巧
$$x \ >> \ n \iff \left \lfloor x \div \ 2^n \right \rfloor \ , \ x的二进制值右移n位$$
$$x \ << \ n \iff x \ \times \ 2^n \ , \ x的二进制值右移n位$$
$$x \ & \ 1 \ == \ 1 \iff x \ % \ 2 \ == \ 1 \ , \ 判断x是否为奇数$$
$$x \ & \ (x -1) \ , \ 清除x最后一位的1$$
$$x \ & \ (-x) \ , \ 得到x最后一位的1$$
经典例题(二进制中1的个数)
问题描述
给定一个正整数n,输出从0到n的每个数的二进制中有多少个1?
输入正整数n
1 | 10 # 输入正整数10 |
算法分析
分析一个数的二进制中有多少个1,可以使用传统的方法,一直模2(mod 2)然后再除以2,知道结果为0即可。这样做虽然也不慢,但是如果二进制中1的个数很少,这样做效率就很低。
可以采用$x \ & \ (x -1)$的方法,每次清除x最后一位的1,清除了多少次即有多少个1。并且使用动态规划的思想,保存之前做过的记录,即求6的二进制位(110)有多少1,将做后一位的1去掉之后为(100),即求4的二进制位有多少1,然后加1即可。
python代码实战
1 | import sys |
代码运行结果

经典例题(N皇后问题)
问题描述
在n×n的国际棋盘上放置彼此不受攻击的n个皇后,按照规则,皇后可以攻击与之在同一行、同一列、统一斜线上的棋子。现在已知又n个皇后,问有多少种不同的放法?
输入皇后的个数n
1 | 6 # 皇后的个数 |
算法分析
之前再深度优先搜索中提到过N皇后的一般解法,确实深度优先是最容易想到的一种做法,但是并不是最快的一种做法,可以尝试采用深度优先+位运算提高效率。
以4皇后为例,每个皇后有四个格子可以放置,可以当作二进制的四个bit。如8(1000)代表皇后放在第1个格子,4(0100)代表皇后放在第二个格子。某一个皇后可以放置的位置由列,斜线和反斜线三个方向限制。
设第i个皇后放置的行数为row,被攻击的列数为col,被攻击的斜线为pie,被攻击的反斜线为na。因此所有被攻击的点为$col \ | \ pie \ | \ na$,因此可以放置的位置为$~(col \ | \ pie \ | \ na) \ & \ ((1 << queen_num) - 1)$,保证高位都为0,不可以放置。
上述操作之后说明该数中二进制位的1就是当前可以放置的位置。每次$x \ & \ (-x)$得到x最后一位的1,并将皇后放置于该位置p,并使用$x \ & \ (x -1)$并将此位的1清除,并进入下一行,下一行被攻击的列为$col \ | \ p$,下一行被攻击的斜线为$(pie \ | \ p) \ << \ 1$,下一行被攻击的反斜线为$(na \ | \ p) \ >> \ 1$
python代码实战
1 | import sys |
代码运行结果

经典例题(斐波那契数列)
问题描述
假设第一个月有一对刚诞生的兔子,第二个月进入成熟期,第三个月开始生育兔子,而一对成熟的兔子每月回生一对兔子,如果兔子永不死去,那么n个月后有多少对兔子?
输入月份数n
1 | 10 # 求第10个月的兔子数 |
算法分析
斐波那契数列是一个典型的算法问题,有多个不同版本的解法,也代表着不同的思想。
首先就是递归解法,根据$f(n)=f(n-1)+f(n-2), \ f(1)=f(2)=1$求解,不过这种解法的时间复杂度为$O(({\frac{\sqrt5 + 1}{2}})^n)$,算f(10)还是非常快的,但是算f(100)简直是天方夜谭。
其次是动态规划解法,建立一个大小为n+1的矩阵,每次计算的值存放于矩阵中此时计算$f(n)=f(n-1)+f(n-2)$时,f(n-1)和f(n-2)就不需要递归计算,只要查表即可,时间复杂度为O(n)。
最快的解法为矩阵解法,根据$\begin{pmatrix} f(n-1) \ f(n) \end{pmatrix} = \begin{pmatrix} 1 & 1 \ 1 & 2 \end{pmatrix} \ \begin{pmatrix} f(n-2) \ f(n-3) \end{pmatrix}$可得
$$\begin{pmatrix} f(\left \lfloor \frac{n}{2} \right \rfloor \times 2) \ f(\left \lfloor \frac{n}{2} \right \rfloor \times 2+1) \end{pmatrix} = {\begin{pmatrix} 1 & 1 \ 1 & 2 \end{pmatrix}}^{\left \lfloor \frac{n}{2} \right \rfloor} \ \begin{pmatrix} 0 \ 1 \end{pmatrix}$$
即问题转化为求矩阵${\begin{pmatrix} 1 & 1 \ 1 & 2 \end{pmatrix}}^{\left \lfloor \frac{n}{2} \right \rfloor}$,时间复杂度为O(n)。乘方问题可以用位运算提高效率,时间复杂度可以提升到O(log(n))
python代码实战
1 | import sys |
代码运行结果
算法总结
位运算说是一种算法,实际上应该说是一种方法。许多问题都可以用位运算来提高效率,位运算很少单独使用,往往同其他的算法一起使用,作为其中的一个步骤,能够在特定的情况下发挥出特殊的效果。